Piximètre synthétise les mesures effectuées sous une forme claire, directement lisible et utilisable, appelée "formule dimensionnelle".
Pour une grandeur étudiée (longueur, largeur ou leur quotient) il est intéressant de connaître l'intervalle dans lequel se situe ses valeurs ainsi que leur moyenne. Une solution incontournable, lorsque ces valeurs deviennent très nombreuses, consiste à les prendre sur un échantillon censé représentatif de la population totale et on écrit traditionnellement, par exemple :
8,1 - 8,8- 9,7
Cependant les statistiques et les probabilités permettent plus de précision en limitant l'incertitude liée au choix d'un échantillon.
Piximètre offre à l'utilisateur la possibilité d'obtenir les résultats suivant l'une ou l'autre méthode, traditionnelle aussi dite classique ici ou statistique. Le passage de l'une à l'autre s'effectue sur le Formulateur, par un clic de souris sur la formule dimensionnelle ou dans les propriétés Avancées de l'onglet Paramètres.
A partir de la version 5.9 Piximètre offre la possibilité d'ajouter le calcul du volume sporique.
La formule classique est calculée par Piximètre en utilisant la méthode simplifiée des déciles. Pour chaque grandeur étudiée :
La formule classique a la forme générale : (Mini) min - max (Maxi) où les valeurs entre parenthèses sont les valeurs exceptionnelles mesurées et min - max sont les bornes de l’intervalle qui correspond à 80% des mesures effectuées (déciles 1 et 9). Les valeurs exceptionnelles ne figurent que si elles sont différentes des bornes de l'intervalle.
En mycologie la formule classique offre une concordance directe avec la plupart des publications (d'où son nom).
En pratique, Piximètre exprime la formule classique sous l'une ou l'autre forme suivante. N'hésitez pas à cliquer (droite et gauche) sur la formule dimensionnelle affichée dans le Formulateur.
La forme développée, comme sur cet exemple :
(4,1) 4,15 - 5,06 (5,1) x (2,8) 3 - 3,8 (4,2) µm
Q = (1) 1,1 - 1,5 (1,6) ; N = 30
Me = 4,62 x 3,45 µm ; Qe = 1,35
Me et Qe (e pour échantillon) sont les valeurs moyennes des mesures.
(4,1) 4,15 -4,62- 5,06 (5,1) x (2,8) 3 -3,45- 3,8 (4,2) µm
Q = (1) 1,1 -1,35- 1,5 (1,6) ; N = 30
La figure ci-dessous montre le principe de découpage de l'échantillon en déciles. Les dix groupes possèdent le même nombre d'éléments mais, évidemment, leurs largeurs peuvent être différentes.
Vue schématique du découpage de l'échantillon en déciles.
La formule dimensionnelle statistique et son calcul |
Sur un échantillon de taille n on calcule la moyenne et l'écart-type me et σe.
Pour la population totale on peut estimer ponctuellement la moyenne m par me et l'écart-type σ par
.
Mais on peut aussi estimer cette population par un intervalle, en supposant que la distribution des valeurs suit une loi normale gaussienne dont les paramètres sont m et σ (Hentic : 178).
Malheureusement l'hypothèse d'une distribution gaussienne ne semble pas toujours pertinente car en regroupant en classes les valeurs de l'échantillon on s'aperçoit que l'histogramme, le plus souvent, n'est pas homogène (Hentic : 176).
Par contre il en va tout autrement pour la moyenne des valeurs : si l'on prend des échantillons suffisamment grands (par exemple de taille n > 30), la moyenne des valeurs des échantillons suit approximativement une loi normale, de paramètres m et 
(Verlant : 124). On accède alors à un intervalle de confiance au seuil c% pour la moyenne de la population.
Par exemple, à partir de l'échantillon choisi, la longueur des spores de champignon, avec c = 95 %
7,9 [8,7 ; 9,1] 9,9 se traduit par :
|
D'une manière générale, dans la formule dimensionnelle statistique de Piximètre, chaque grandeur (longueur, largeur et quotient) est notée :
Min [m ; M] Max
où :
[Min Max] | est un intervalle centré sur la moyenne de l'échantillon. Au seuil de c %, il a un rayon |
[m ; M] | est l'intervalle de confiance sur la moyenne de la population. Il est centré sur la moyenne de l'échantillon et, au seuil c %, il a un rayon |
Insistons encore sur la nécessité de travailler avec des échantillons de grande taille, par exemple 30. En dessous, la méthode ne fournit plus de résultats sûrs au même seuil de confiance. |
En pratique Piximètre exprime la formule statistique sous l'une ou l'autre forme suivante.
La forme développée, comme sur cet exemple :
11,4 [14,6 ; 15,4] 18,6 x 11,4 [14,6 ; 15,3] 18,6
Q = 0,9 [1] 1,1 ; N = 100 ; C = 95%
Me = 15 x 15 ; Qe = 1
Cet exemple montre pour Q un intervalle de la moyenne de la population (en vert) dont les deux bornes sont égales. Dans ce cas Piximètre remplace ces deux bornes par une seule. Sur la troisième ligne Me et Qe (e pour échantillon) sont les valeurs moyennes des mesures, comme dans le cas de la formulation classique.
La forme concise, comme ceci, au choix de l'utilisateur :
11,4 [14,6 -15- 15,4] 18,6 x 11,4 [14,6 -15- 15,3] 18,6
Q = 0,9 [ -1- ] 1,1 ; N = 100 ; C = 95%
Ici les bornes de l'intervalle de la moyenne de la population (en vert) n'apparaissent que si elles sont différentes de la valeur moyenne. L'expression de Q sur cet exemple est caractéristique et remplace la forme [1 -1- 1]. L'augmentation du nombre de décimales du résultat peut changer cette expression.
Avec d'autres échantillons de même effectif on obtiendrait de nouveaux intervalles de confiance de cette moyenne m, avec le même coefficient de confiance. Tous auraient la même amplitude 
.
Voici quelques exemples :
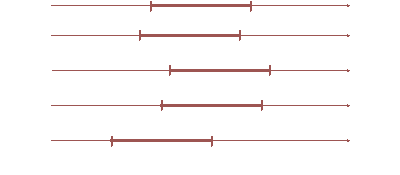 | Si l'on prélevait un très grand nombre de tels échantillons, environ 95% d'entre eux contiendraient la moyenne inconnue m de la population. En fait, on n'en prélève qu'un seul et on ne peut pas savoir de manière certaine si celui-ci contient ou non le nombre m, mais la méthode mise en œuvre permet d'obtenir un "bon" intervalle dans 95% des cas. Un "bon" intervalle contient m. |
Soit n valeurs de la grandeur étudiée (longueur, largeur et quotient) on obtient la moyenne arithmétique me et l'écart-type σe par les formules classiques :
|
moyenne m = me ----- et -----écart-type |
| a | ||
k(c) = 1,96 au seuil de 95 % (1 au seuil de 68 %).
|
 fig. 1 : Clic droit sur la formule. | Piximètre fournit en complément la valeur de l'écart-type calculé sur chaque échantillon. Cette information est ajoutée à la formule dimensionnelle comme indiqué, encadré en rouge, sur la figure 1 ci-contre. sxy est l'écart-type calculé sur les séries respectivement X et Y. Cette information n'est disponible que sur la formule statistique, par un Clic droit sur la formule et "Infos +". Elle est copiée avec la formule. |
L'expérience montre qu'en mycologie, pour la mesure des spores de champignons, il n'est pas rare que la réalisation d'un grand nombre de mesures (100 - 200, voire plus) conduise à visualiser la fameuse courbe en cloche de la loi normale, ce qui valide d'autant mieux les résultats de la formulation statistique. Piximètre est capable de gérer sans difficulté un très grand nombre de mesures.
Les échantillons obtenus sont répartis en classes (typiquement neuf classes) matérialisées par des histogrammes (figure 2 ci-contre). Pour les voir, appuyez sur HDi dans le volet Formulateur.
Comme indiqué plus haut, l'intervalle rouge [Min, Max] de la formule statistique n'est correct que dans le cas d'une distribution normale des valeurs de l'échantillon, alors que l'intervalle vert [m ; M] lui, est toujours valable quelque soit cette loi.
Piximètre vérifie la normalité de la loi de distribution des échantillons et allume le feu vert du Formulateur lorsque c'est le cas. Il met en œuvre deux méthodes complémentaires pour vérifier cette normalité :
Le résultat des vérifications est reporté sur l'histogramme (figure 2). Le contenu des quatre intervalles ci-dessus est respectivement noté i, j, k et l. L'homogénéité est notée ho. Ces notations sont reportées en rouge lorsqu'elles sont en dehors des limites de tolérance définies. Le feu de chaque histogramme n'est allumé en vert que si l'échantillon est normal.
Le voyant général du Formulateur ne s'allume en vert que lorsque les échantillons X et Y sont NORMAUX. Il s'allume en orange si l'un des deux seulement est normal et, sinon, reste éteint.
Sur l'histogramme Y de la figure 2 ci-dessus, i = 76 + (en rouge) signifie que l'intervalle i (m ± s) de l'échantillon Y comporte 76% des valeurs de l'échantillon, ce qui est + que défini (par défaut [64%, 75%]). La loi correspondante n'est vraisemblablement pas normale bien que l'histogramme soit homogène (ho n'est pas rouge). En conséquence le feu de l'histogramme Y s'allume en rouge ce qui entraine que le feu général du Formulateur ne s'allume pas en vert mais en orange (dans notre exemple, puisque X est vert).
Notez bien : L’intervalle fourni en rouge par Piximètre, dans sa formule dimensionnelle statistique, n’est valable que dans le cadre d’une population normale attestée par un échantillon normal. Il est entendu, par contre, que l’intervalle sur la moyenne est toujours valable puisqu’il existe une loi normale pour les moyennes.
Dans le cas de la mesure d'une seule dimension (X ou Y) Piximètre affiche le voyant en fonction du seul échantillon significatif.
Concernant l'étude des champignons, certaines publications récentes font référence à d’autres paramètres, dont le volume sporique. Jean-Louis JALLA, mycologue expérimenté, a attiré notre attention sur l'intérêt de l'ajouter à la formule dimensionnelle calculée par Piximètre. Il est certain que cette donnée est très significative et varie beaucoup entre des espèces proches.
La formule de calcul du volume sporique actuellement utilisée en mycologie tend à assimiler les spores à des ellipsoïdes de révolution, ce qui n’est bien entendu qu'une vue théorique. Ce volume sera d’autant plus juste que la forme des spores se rapprochera le plus possible de cette structure parfaite. Pour les formes réelles, le volume calculé sera donc entaché d’une erreur ± importante, fonction de leur éloignement de l'ellipsoïde. Néanmoins il pourra quand même servir de référence à condition bien sûr d’avoir toujours à l’esprit les limites de la méthode.
La formule retenue pour le calcul de ce volume est :
où l et L représentent respectivement la petite et la grande dimension des objets mesurés.
Attention cependant, une erreur de mesure des dimensions a des répercutions importante sur le volume. Par exemple, pour une spore de dimension 8,5 x 10 µm le volume calculé est de 378 µm3, il devient 445 µm3 pour simplement 0,5 µm d’erreur par excès sur les deux dimensions. L’intérêt d’une étude portant sur un nombre important de mesures est ici évident, la composante aléatoire de l’erreur de mesure est pondérée par la moyenne. Il est également évident que l’erreur systématique de mesure (par exemple erreur d’étalonnage de Piximètre) existe toujours, d’où l’intérêt d’un étalonnage le plus rigoureux possible.
Piximètre calcule ce volume sporique et le traite suivant la méthode d'affichage choisie (classique ou statistique) pour l'ajouter à la formule dimensionnelle qui prend, par exemple, la forme suivante :
 fig. 3 : Affichage du volume. | Le volume V est ajouté, ici sous forme classique, avec le volume moyen Ve calculé sur l'échantillon. Le menu contextuel (clic droit sur la formule) permet d'afficher ou non le volume. comme montré sur l'image. Toutes les informations affichées par le Formulateur sont copiées ou enregistrées par les boutons correspondants, comme les autres données. |
HEINEMANN P. & RAMELOO J. 1985 - De la mesure des spores et de son expression. AGARICA, vol. 6, n°. 12, pp. 366-380.
HENTIC René. 2000 - A propos de l'exploitation statistique des mesures en mycologie. Bull. Soc. Mycol. Fr., 116(2), p. 173-180.
JALLA J.L. - Mesure des spores et interprétation statistique des résultats obtenus. Internet
VERLANT B. & SAINT-PIERRE G. 1997 - Statistique et probabilités tome 2, BTS industriels. Éd. Foucher. Paris
et les valeurs Min et Max sont ses bornes. Il signifie qu'il y a c % de chance que la valeur de la grandeur étudiée soit comprise entre Min et Max.
et les valeurs m et M sont ses bornes. Il signifie qu'il y a c % de chance que cet intervalle contienne la moyenne des valeurs de la grandeur étudiée sur l'ensemble de la population.
----et------
